2022년02월19일 1번
[자연과학개론] 그림과 같이 곡선과 반지름 R인 원으로 구성되어 있는 궤도의 높이 h인 곳에 구슬을 가만히 놓으면 구슬은 궤도를 따라 미끄러지며 운동하여 원궤도의 두 지점 A와 B를 지난다. A, B에서 원궤도가 구슬에 작용하는 수직항력은 각각 nA, nB 이다.
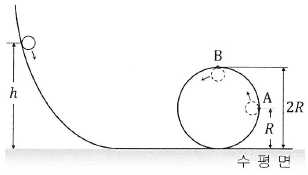
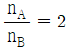일 때, h는? (단, 중력 가속도는 일정하고, 구슬의 크기, 공기 저항과 모든 마찰은 무시한다.)
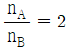일 때, h는? (단, 중력 가속도는 일정하고, 구슬의 크기, 공기 저항과 모든 마찰은 무시한다.)-
①
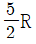
- ② 3R
-
③
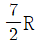
- ④ 4R
-
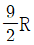
(정답률: 알수없음)
문제 해설
이전 문제
다음 문제
원의 중심에서 구슬까지의 거리를 r이라고 하면, 중력과 수직항력의 평형을 이루기 위해서는 다음과 같은 관계가 성립한다.
mg = nAsinθ + nBsinθ
mg = 2nAsinθ
r = R(1-cosθ)
여기서 θ는 원의 중심에서 구슬까지의 각도이다.
따라서, h = R - r = R - R(1-cosθ) = R(1-cosθ) 이다.
보기에서 정답이 "4R" 인 이유는, θ가 60도일 때, h가 최대값인 R x 3이 되기 때문이다. 따라서, h는 4R보다 작을 수 없다.